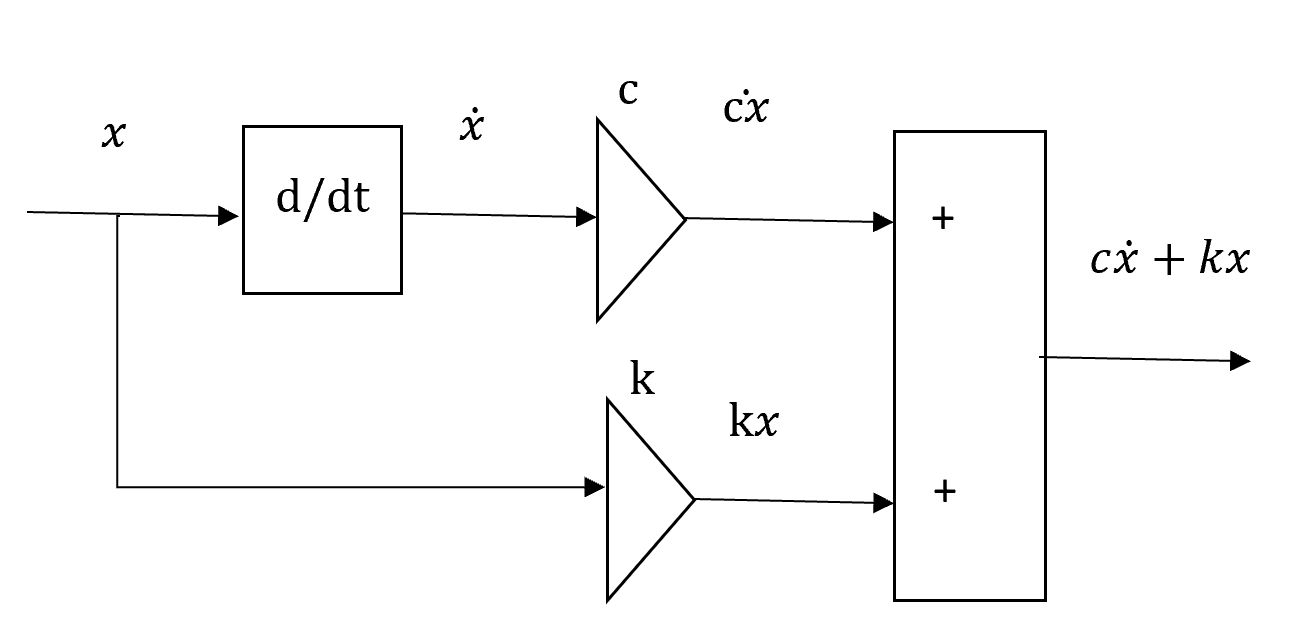
Examen de Vibrations 27/12/2022 - Exercice 1
Exercice sur l'utilisation d'un isolateur. On donne une machine qui transmet une force importante au sol qu'on voudrait limiter à 10 KN à cause d'un balourd qui tourne à une certaine vitesse. On démontre qu'avec un seul isolateur, le problème ne pas être résolu. Avec deux isolateurs en série la force transmise est limite. La société ne disposant que d'un seul isolateur, la solution serait d'augmenter la masse totale. On calcule la masse à ajouter pour que la force transmise soit acceptable.