aannaque's blog

Articles

Affichage des articles du mai, 2019

How to determine eigenvalues and eignevectors of a matrix in Excel

mai 28, 2019

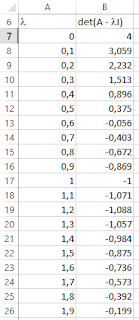
We would like to compute the eigenvalues and eigenvectors of the following matrix in Excel. BTW Excel does not have any native function that can do that. $\begin{bmatrix} 2 & -1 & 0\\-1 & 2 & -1\\0 & -1 & 2\end{bmatrix}$ The characteristic polynomial of this matrix is : $det( A - \lambda I)$ qui donne $(2 - \lambda)(2 - \sqrt{2} - \lambda)(2 + \sqrt{2} - \lambda)$ . The analytical eigenvalues solutions are: $\lambda_1=2 - \sqrt{2}=0.58578644$ , $\lambda_2=2$ and $\lambda_3=2 + \sqrt{2}=3.41421356$ The eigenvectors are : $\begin{Bmatrix} 1 \\ \sqrt{2}\\1\end{Bmatrix}$ , $\begin{Bmatrix} 1 \\0\\-1\end{Bmatrix}$ and $\begin{Bmatrix} 1 \\-\sqrt{2}\\1\end{Bmatrix}$ Procedure 1 st method We start by creating two columns, one for l (from 0 to 4) and the other for $det( A - \lambda I)$ Then we plot $det( A - \lambda I) = f(\lambda)$ We can c...

Calcul des valeurs propres et vecteurs propres sur Excel

mai 26, 2019

On voudrait calculer les valeurs propres et les vecteurs propres de la matrice suivante sur Excel qui ne comporte aucune fonction native pour faire ce calcul. $\begin{bmatrix} 2 & -1 & 0\\-1 & 2 & -1\\0 & -1 & 2\end{bmatrix}$ Son polynôme caractéristique est est $det( A - \lambda I)$ qui donne $(2 - \lambda)(2 - \sqrt{2} - \lambda)(2 + \sqrt{2} - \lambda)$ . Théoriquement les valeurs propres sont $\lambda_1=2 - \sqrt{2}=0.58578644$ , $\lambda_2=2$ et $\lambda_3=2 + \sqrt{2}=3.41421356$ Et les vecteurs propres sont : $\begin{Bmatrix} 1 \\ \sqrt{2}\\1\end{Bmatrix}$ , $\begin{Bmatrix} 1 \\0\\-1\end{Bmatrix}$ et $\begin{Bmatrix} 1 \\-\sqrt{2}\\1\end{Bmatrix}$ Procédure 1 ère méthode On peut créer deux colonnes, une pour l (de 0 à 4) et l’autre pour $det( A - \lambda I)$ Puis on trace $det( A - \lambda I) = f(\lambda)$ On peut voir ou se trouvent les trois zéros de la fonction tracée. Pour plus...