aannaque's blog

Application de la méthode de Jacobi pour trouver les valeurs et vecteurs propres d'un système à plusieurs degrés de liberté en appliquant des rotations successives.

Application de la méthode de déflation et de la puissance itérée pour trouver les modes supérieurs

Méthode de la puissance itérée pour obtenir la première valeur propre et le premier vecteur propre d'un système à plusieurs degrés de liberté.

Quotient de Rayleigh d'un système à plusieurs degrés de liberté

L'objectif est de trouver la matrice de flexibilité par la méthode des coefficients d'influence et sans inverser la matrice raideurs.

La méthode de Stodola permet d'obtenir soit la première ou la dernière valeur propre d'un système à N degrés de liberté. Dans cette vidéo, la méthode de Stodola est appliquée sur Excel.  

 Comment obtenir la matrice des raideurs d'un système à trois degrés de liberté ?

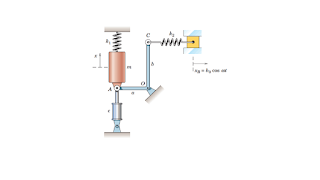
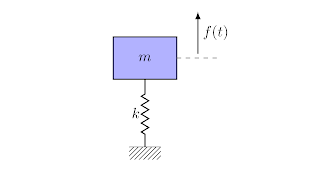
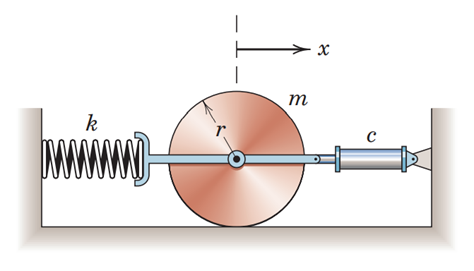
  Examen 2021-2022, exercice 3: L'instrument représenté sur la figure a une masse de 43 kg et est monté sur quatre ressorts identiques de raideur chacun 7.2 KN/m. Le mouvement du sol est harmonique. Q1 Calculer la fréquence propre du système (en Hz) Q2 Si l'amplitude de vibration verticale de la base est de xB = 0.10 mm, calculer la plage de fréquences (en Hz) de la base à éviter pour que le déplacement de l’instrument ne dépasse pas 0.15 mm. Q3 Quand la fréquence d’excitation se trouve dans l’intervalle calculé, serait-il bénéfique ou pas d’ajouter un amortisseur ? (Pour argumenter vous n’avez pas besoin de développer des calculs laborieux) Q4 Un ingénieur a posé un autre instrument de masse 17 Kg sur le premier. Quelle est la conséquence sur la gamme de fréquence calculée précédemment ?

  Examen 2021-2022, Exercice 2 Enoncé : Un système mécanique est composé d’une masse m qui se déplace verticalement, d’un ressort de raideur k1 et d’un amortisseur de coefficient c. Le système est excité par une force au point A due à un mouvement harmonique imposé à l’extrémité droite du ressort de raideur k2. Les tiges OA et OC sont sans masses, articulées au point O et elles sont toujours perpendiculaires. Le déplacement de la masse est mesuré par rapport à la position d’équilibre. En l’absence du mouvement imposé (dans ce cas la tige OA est horizontale et OC est verticale). On suppose de petites oscillations autour de la position d’équilibre.

  Examen 2021-2021 de Vibrations. Exercice 1 Enoncé : Un système masse ressort (sans amortisseur) est sollicité par une force f(t) continue et dérivable. La solution particulière est notée xp(t) qui est de même nature que la force. f est aussi continue et dérivable. Trouver la condition sur les conditions initiales x0 et v0 pour que la solution transitoire n’apparaisse pas dans la solution totale.

Examen de vibrations 2021-2022. Exercice 4 Un cylindre de masse 50 Kg est entrain de rouler sans glisser sur le sol. Il est aussi lié à gauche à un ressort de raideur 75 N/m et à droite à un amortisseur de constante 10 N s/m. Le rayon du cylindre est r=0.5 m. Rappel : Le moment d’inertie d’un cylindre par rapport à l’axe passant par son centre est J=(mr^2)/2. 1 Dans un premier temps on ne tient pas compte de la présence de l’amortisseur. Trouver l’équation de mouvement à partir de l’énergie cinétique et potentielle du système. 2 Ajouter la force due à l’amortisseur en reprenant le terme dû au ressort et en remplaçant k par c et x par dx/dt 3 Retrouver la même équation de mouvement en appliquant le PFD (incluant aussi l’effet de l’amortisseur) 4 Trouver la pulsation propre wn en fonction de k et m, le taux d’amortissement zeta en fonction de c, m et wn et la pulsation amortie wd en fonction de wn et zeta. 5 A l’instant t=0, le cylindre est écarté de sa position d’équilibre de x0=-0.2 m