Analyse de Fourrier sur Excel

Est-il possible de faire l’analyse de Fourier dans Excel ? C’est-à-dire peut-on connaitre le contenu fréquentiel d’un signal ? La réponse c’est oui.

Pour cela nous allons utiliser un outil très puissant « l’utilitaire d’analyse ». Avant de continuer ce tutoriel vérifiez que vous avez cet outil activé. Sur le ruban Données, dans la rubrique analyse, vérifier la présence de l’utilitaire d’analyse.

Sinon, dans les options, Cliquer sur Compléments puis en bas dans Gérer choisir Compléments Excel et cliquer sur le bouton atteindre.

Vérifier que la case à cocher Analysis ToolPak est choisie

L’utilitaire d’analyse comporte beaucoup d’outils. Celui que l’on va voir dans ce tutoriel est la FFT (Transformation de Fourier Rapide). La FFT est un algorithme de calcul de la transformée de Fourier discrète (par opposé à continue) car on manipule une fonction connue en un nombre limité de points. L’algorithme est très rapide lorsque le nombre de points de l’échantillon est une puissance de 2. D’ailleurs l’outil que nous allons utiliser exige que le nombre soit une puissance de 2.

Génération d’un signal de fréquence connu

Nous allons remplir les différentes cellules avec les informations qui vous nous permettre de générer notre signal et calculer sa FFT.

Paramètre	Valeur	Signification
f	10 hz	Fréquence du signal à générer
T=1/f	0.1 s	Période du signal
fs	1000 hz	Fréquence d’échantillonnage
Ts	0.001 s	Temps séparant deux points de m’échantillon
N	128	Nombre de points 2^7
fstep=fs/N	7.8125	Le pas dans le domaine fréquentiel

Nous allons ensuite générer deux colonnes qui correspondent à l’abscisse et l’ordonné de notre signal. t commence à partir de 0 et est incrémenté de Ts et y contient la formule : =SIN(2*PI()*$B$1*A7)

Après avoir copié la formule sur les 128 cellules, on trace la variation de y en fonction de t

Noter que la durée de notre échantillon n’est pas un multiple de la période (0.1 s). Cela va générer un problème dit de fuite.

Cliquons maintenant sur l’outil d’analyse et choisissons Transformation de Fourier Rapide (FFT).

Dans Plage d’entrée on spécifie les valeurs correspondant à y et on désigne une plage ou le calcul de la FFT va être affiché.

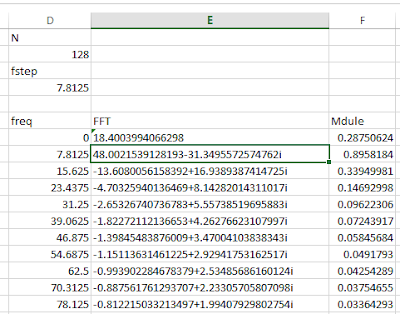
Le résultat des calculs est affiché dans la colonne E. Noter que la FFT est complexe. Pour calculer son module on utilise la fonction COMPLEXE.MODULE(). Donc sur la colonne freq on génére le vecteur des fréquences commençant à 0 et ayant un pas de fstep. La formule dans F7 par exemple est =2*COMPLEXE.MODULE(E7)/$D$2

La FFT est symétrique par rapport au milieu. Il suffit de la tracer entre 0 et N.fs/2.

En zoomant

On trouve que la fréquence dominante est 7.8125 Hz. Nous avons aussi une composante continue (f=0 Hz) et d’autres composantes dont le module décroit avec la fréquence. Nous n’avons pas trouvé notre fréquence 10 Hz que nous avons utilisé pour générer le signal. C’est le phénomène de fuite évoqué plus haut.

Pour éviter le phénomène de fuite il faut que la durée de l’échantillon soit un multiple de la période du signal. Changeons les valeurs des paramètres

Paramètre	Valeur	Signification
f	10 hz	Fréquence du signal à générer
T=1/f	0.1 s	Période du signal
fs	1280 hz	Fréquence d’échantillonnage
Ts	0.00078125 s	Temps séparant deux points de m’échantillon
N	128	Nombre de points 2^7
Fstep=fs/N	10	Le pas dans le domaine fréquentiel

Notre signal correspond exactement à une période

On recalcule la FFT et son module. On remarque qu’on obtient une seule raie qui correspond à la fréquence de notre signal

Si on ajoute du bruit à notre signal (y=sin(2pf t) + 0.6*ALEA())

La FFT donne

La fréquence dominante reste f=10 Hz

Somme de deux signaux périodiques

Dans cette partie, nous considérons un signal de type y=sin (2pft) + sin(2p(4f)t) composé d’un signal de fréquence f et d’un autre de fréquence 4f.

Le calcul du module de la FFT donne

On voit bien que notre signal est composé de deux signaux l’un à 10 Hz et l’autre à 40 Hz

Si la deuxième composante a une fréquence de 4.5 f au lieu de 4 f, on obtient :

La première fréquence est correcte mais on a l’impression que le signal contient deux fréquences à 40 et 50 Hz. L’explication est que la durée de l’échantillon correspond bien à une période pour le signal à 10 Hz mais à 4.5 périodes pour le deuxième.

Pour résoudre le problème, il faut que la durée du signal soit un multiple des périodes de ses composantes.

Pour une durée de 0.2s, on obtient deux périodes du signal à 10 Hz et 9 périodes du signal à 45 Hz

Et le calcul de la FFT donne

Parfait ! On obtient nos deux composantes à 10 Hz et 45 Hz.

En général pour le mélange de deux signaux de fréquences f1 et f2, la période doit être =PPCM(f1;f2)/f1/f2

FFT de signaux importés

Dans mon cas j’ai simulé un système masse ressort et j’ai importé les données dans Excel. Les données brutes sont données sur la figure suivante :

On remarque qu’il y a une fréquence dominante qui correspond à la fréquence propre du système masse ressort (dans mon cas m=1 kg, k=25 N/m donc f=0.796 Hz)

Si on tronque le signal de façon à avoir le nombre de points une puissance de deux, la durée ne va pas correspondre à un multiple de la vrai période du signal et donc nous allons avoir le problème de fuite. De même si on tronque le signal de façon à avoir la durée qui correspond à un multiple de la période le nombre de points obtenus ne sera pas nécessairement une puissance de 2. Ce que nous pouvons faire c’est de tronquer le signal pour avoir trois oscillations puis le re-échantillonner pour avoir un nombre de points une puissance de deux (256 par exemple).

Si le temps importé est dans la plageB2 :B410 et les ordonnés importés sont dans la plage D2 :D410,

on génère un nouveau signal de fréquence d’échantillonnage 256/T avec T la durée du signal tronqué (dans notre cas fs=256/4.08=62.74 et Ts=0.0159 s).

On génère un nouveau tableau de temps contenant 256 valeurs commençant à 0 et de pas Ts.

On doit alors calculer les nouvelles valeurs de y2 qui correspondent au nouveau vecteur temps. La formule semble compliquée mais en fait on fait un simple calcul d’interpolation

La formule est :

=INDEX(D2:D410;EQUIV(J2;B2:B410;1))+(INDEX(D2:D410;EQUIV(J2;B2:B410;1)+1)-INDEX(D2:D410;EQUIV(J2;B2:B410;1)))*(J2-INDEX(B2:B410;EQUIV(J2;B2:B410;1)))/ ((J2-INDEX(B2:B410;EQUIV(J2;B2:B410;1)+1))-INDEX(B2:B410;EQUIV(J2;B2:B410;1)))

Par exemple EQUIV(J2;B2:B410;1) donne le rang de l’élément du tableau B2:B410 juste supérieur à J2. INDEX(D2:D410;EQUIV(J2;B2:B410;1)) donne la valeur de y2 qui correspond au rang trouvé.

On obtient de nouveaux paramètres Ts=0.0159 et fs=62.745

On trouve une fréquence de 0.73529 soit une erreur de 7.5 %